Fähigkeiten für Integralaufgabe
Für die Integralaufgabe müssen Sie die entsprechenden Integrationsregeln kennen, nämlich:
• Das Bestimmen einer Stammfunktion.
- Sie müssen also elementare Funktionen „aufleiten“ können.
- Insbesondere sollten Sie die Potenzregel für Integrale kennen.
• Die „Kettenregel rückwärts“, genauer: Lineare Substitution
• den „Hauptsatz“ (der Differenzial- und Integralrechnung)
Sie sollten außerdem das Bestimmen einer Fläche mit Hilfe von Integralen beherrschen.
Stammfunktionen
In gewissem Sinne dürfen Sie die Integralrechnung als Umkehrung der Differenzialrechnung verstehen.
Während man in der Differenzialrechnung ableitet, geht man in der Integralrechnung den umgekehrten Weg
und "leitet auf". Der Fachbegriff ist Stammfunktion. Man sucht also zu einer
gegebenen Funktion f(x) eine Stammfunktion F(x). Damit ist der Zusammenhang f(x)=F'(x) sofort ersichtlich.
Die Integrationskonstante C
Es soll eine Stammfunktion zu f(x)=2x gefunden werden. Nun ist (x2)'=2x, deshalb
ist F(x)=x2 eie Stammfunktion von f(x). Nun gilt aber auch (x2+1)'=2x und
(x2-5)'=2x, so dass auch F(x)=x2+1 und F(x)=x2-5 Stammfunktionen sind.
Sie sehen also, dass Stammfunktionen im allgemeinen nicht eindeutig sind. Man sagt: Eine Stammfunktion
sei bis auf eine Konstante (die so genannte Integrationskonstante C) unbestimmt.
Hinweis:
Wenn Sie in den Abi-Aufgaben eine Stammfunktion bestimmen sollen, so vergessen Sie
die Integrationskonstante C nicht!
Tabelle mit elementaren Stammfunktionen
| f(x) | F(x) = ∫f(x)dx |
| c | cx+C |
| xn | 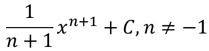 |
| sin(x) | -cos(x)+C |
| cos(x) | sin(x)+C |
| 1/x | ln(|x|)+C |
| ex | ex |
Tabelle mit Integrationsregeln
| Bezeichnung | Rechenregel |
| Konstanter Faktor: | ∫c·f(x)dx = c·∫f(x)dx |
| Summenregel: | ∫(f(x)+g(x))dx = ∫f(x)dx + ∫g(x)dx |
| Kettenregel "rückwärts": | 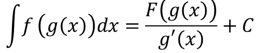 Nur wenn g(x) linear ist, d.h. g(x)=mx+c gilt! |
Abi-Aufgaben früherer Jahrgänge
Pflichtteil 2010 - Aufgabe 2:
Berechnen Sie das Integral
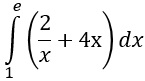 .
.
(2 VP)
Pflichtteil 2009 - Aufgabe 2:Berechnen Sie das Integral
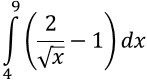 .
.
(2 VP)
Pflichtteil 2008 - Aufgabe 2:G ist eine Stammfunktion der Funktion g(x) mit g(x)=2-3·sin(4x).
Der Punkt P(0|1) liegt auf dem Schaubild von G.
Bestimmen Sie einen Funktionsterm von G.
(2 VP)
Lösungen in Kurzform:Die vollständigen Lösungewege werden im Video gezeigt.
Pflichtteil 2010 - Aufgabe 2: 2e2)
Pflichtteil 2009 - Aufgabe 2: -1
Pflichtteil 2008 - Aufgabe 2:
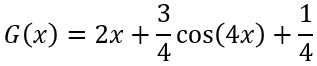
| Downloads |
PowerPoint